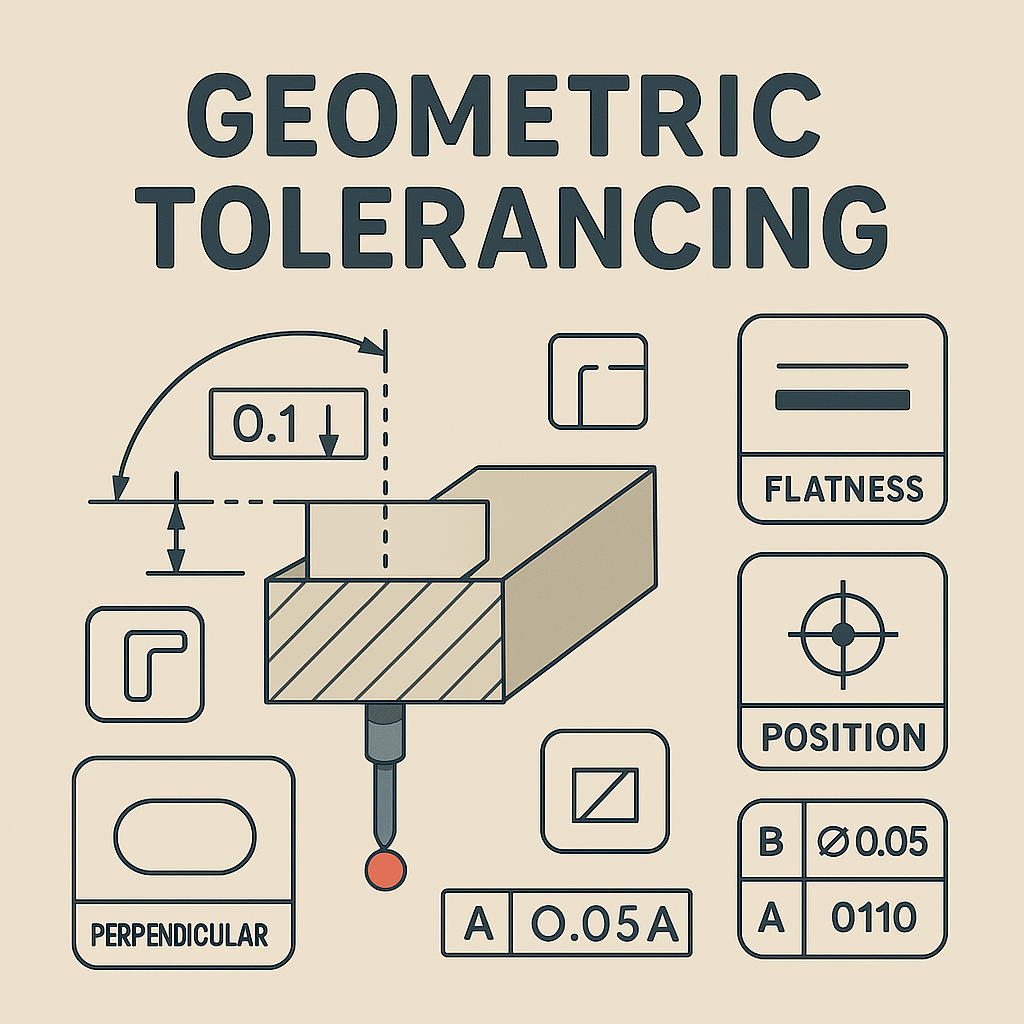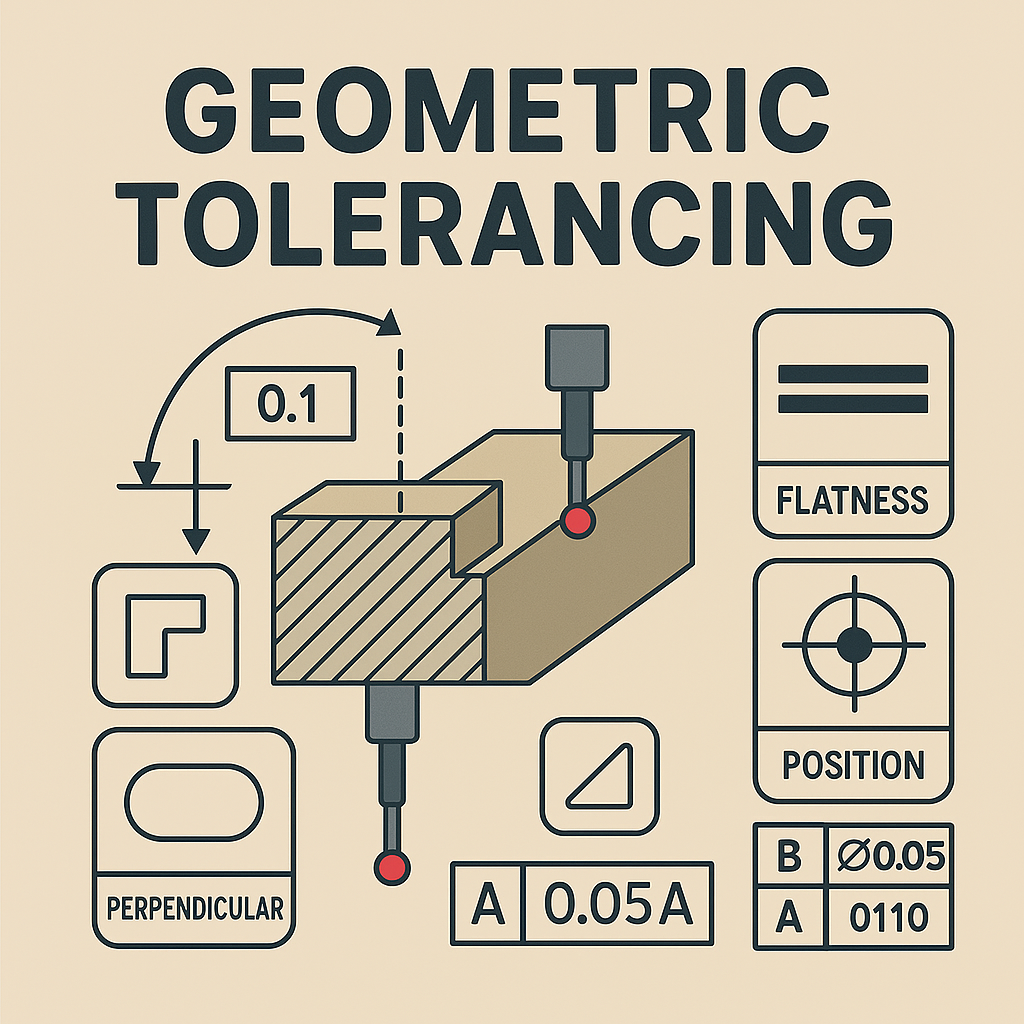
幾何公差（Geometric Dimensioning and Tolerancing: GD&T）は、設計図面において、部品の形状、寸法、位置、姿勢、振れなどの幾何学的特性の許容範囲を規定するための国際的な規格です。従来の寸法公差に加えて、より厳密かつ明確に部品の機能を定義し、製造、検査、組み立てにおける誤解や曖昧さを排除することを目的としています。

幾何公差の基本概念

幾何公差は、部品の理想的な形状や位置からの許容されるばらつきの範囲を、公差域（Tolerance Zone）という概念を用いて定義します。この公差域は、点、線、面、または空間として規定され、部品の実際の幾何学的特性がこの公差域内に収まっている場合に、その部品は許容範囲内であると判断されます。

幾何公差は、以下の主要な要素で構成されています。

1. 幾何公差記号（Geometric Characteristic Symbol）: どの幾何学的特性に公差が適用されるかを示す記号です。例えば、真直度、平面度、円筒度、位置度、同軸度などが挙げられます。
2. 公差域指示記号（Tolerance Zone Symbol）: 公差域の形状や種類を示す記号です。例えば、直径、半径、平行平面間などが挙げられます。
3. 公差値（Tolerance Value）: 許容されるばらつきの大きさを示す数値です。
4. データム指示記号（Datum Feature Symbol）: 部品の基準となる幾何学的特性（データム）を示す記号です。データムは、他の幾何学的特性の評価や測定の基準となります。
5. データム識別子（Datum Feature Identifier）: 特定のデータムを示すアルファベットです。
6. 幾何公差枠（Feature Control Frame）: 上記の要素を組み合わせて、一つの幾何公差の要件を記述するための枠です。

幾何公差の種類と記号

幾何公差は、その特性によっていくつかのカテゴリに分類されます。

形状の公差（Form Tolerances）

形状の公差は、個々の幾何学的要素の形状のばらつきを規制します。データムは使用されません。

• 真直度（Straightness）: 線状の幾何学的要素が、指定された長さにおいて、理想的な直線からどれだけ逸脱してよいかを規定します。公差域は、平行な2つの直線または直径で示される円筒です。
• 平面度（Flatness）: 平面状の幾何学的要素が、指定された領域において、理想的な平面からどれだけ逸脱してよいかを規定します。公差域は、平行な2つの平面です。記
• 真円度（Circularity / Roundness）: 円または円筒の断面が、理想的な円からどれだけ逸脱してよいかを規定します。公差域は、同心円で囲まれた領域です。
• 円筒度（Cylindricity）: 円筒面が、理想的な円筒からどれだけ逸脱してよいかを規定します。公差域は、同軸な2つの円筒で囲まれた領域です。

姿勢の公差（Orientation Tolerances）

姿勢の公差は、2つ以上の幾何学的要素間の角度関係や平行関係、垂直関係のばらつきを規制します。データムが使用されます。

• 平行度（Parallelism）: ある幾何学的要素が、データムとなる別の幾何学的要素に対して、指定された距離で平行であるべき範囲を規定します。公差域は、平行な2つの平面または円筒です。
• 直角度（Perpendicularity）: ある幾何学的要素が、データムとなる別の幾何学的要素に対して、指定された角度（通常は90度）で垂直であるべき範囲を規定します。公差域は、平行な2つの平面または円筒です。
• 傾斜度（Angularity）: ある幾何学的要素が、データムとなる別の幾何学的要素に対して、指定された角度で傾いているべき範囲を規定します。公差域は、平行な2つの平面または角度を持つ2つの線です。

位置の公差（Location Tolerances）

位置の公差は、点の中心、軸線、または平面の中心面などの幾何学的要素の、データムに対する正確な位置からのばらつきを規制します。

• 位置度（Position）: 穴、ピン、その他のフィーチャーの中心軸線または中心面が、データムによって定義された理論的な正確な位置からどれだけ離れてよいかを規定します。公差域は、通常、直径または幅で示される円または平行平面です。
• 同軸度（Concentricity / Coaxiality）: 2つ以上の円筒または円の軸線が、共通のデータム軸線に対してどれだけ同軸であるべきかを規定します。公差域は、データム軸線を中心とする円筒です
• 対称度（Symmetry）: 部品のフィーチャー（例えば、ノッチやスロット）の中心面が、データムの中心面に対してどれだけ対称であるべきかを規定します。公差域は、データムの中心面を中心とする2つの平行な平面です。

振れの公差（Runout Tolerances）

振れの公差は、部品をデータム軸またはデータム点周りに回転させたときに、指定された表面がどれだけ変動してよいかを規定します。

• 円周振れ（Circular Runout）: 部品を固定された軸を中心に回転させたときに、測定面上の指示器の読み取り値の変動幅が、指定された円周上のどの位置でも公差値を超えてはならないことを規定します。個々の円周要素に適用されます。
• 全振れ（Total Runout）: 部品を固定された軸を中心に回転させたときに、測定面全体の指示器の読み取り値の変動幅が、公差値を超えてはならないことを規定します。部品のすべての円周要素および軸方向の要素に同時に適用されます。

データム（Datum）

データムは、幾何公差を適用する際の基準となる、部品上の理論的に正確な幾何学的要素（点、線、面）です。データムは、通常、部品の機能上重要な面や軸線などが選ばれます。

データムは、データムフィーチャー（Datum Feature）と呼ばれる実際の部品の幾何学的特性に対応します。データムフィーチャーは、必ずしも理想的な形状を持っているわけではないため、データムターゲット（Datum Target）やデータムシミュレータ（Datum Simulator）といった概念を用いて、データムを確立します。

データムは、幾何公差枠の中で、データム識別子（A、B、Cなどのアルファベット）を用いて指定されます。複数のデータムを使用する場合、その順序は拘束の優先順位を示します。例えば、A-B-Cという順序の場合、最初にデータムAで位置決めを行い、次にデータムBで姿勢を拘束し、最後にデータムCで回転を拘束します。

最大実体公差方式（Maximum Material Condition: MMC）と最小実体公差方式（Least Material Condition: LMC）

幾何公差では、部品の寸法が最大実体状態（Maximum Material Condition: MMC）または最小実体状態（Least Material Condition: LMC）にある場合に、幾何公差の値を大きくすることができる場合があります。

• 最大実体状態（MMC）: 穴の場合は最小径、軸の場合は最大径など、そのフィーチャーが最も多くの材料を含む状態です。MMCを示す記号は「Ⓜ」です。
• 最小実体状態（LMC）: 穴の場合は最大径、軸の場合は最小径など、そのフィーチャーが最も少ない材料を含む状態です。LMCを示す記号は「Ⓛ」です。
• 実効状態（Virtual Condition）： MMCまたはLMCにあるフィーチャーと、それに適用される幾何公差によって形成される、理論的な境界です。

MMCやLMCを適用することで、部品の組み立てや機能性を損なうことなく、製造公差を緩和できる場合があります。これは、例えば、穴と軸の嵌め合いにおいて、穴が大きく、軸が小さい場合に、位置のずれが多少大きくても組み立てが可能になるという考え方に基づいています。

投影公差域（Projected Tolerance Zone）

位置の公差が適用される穴などに、ボルトやピンなどが挿入される場合、そのボルトやピンが相手部品と正しく嵌合するためには、穴の軸線のばらつきが一定の範囲内に収まっている必要があります。投影公差域は、穴の表面から一定の距離だけ投影された領域に公差域を設定することで、この嵌合性を保証します。投影公差域を示す記号は「Ⓟ」です。

幾何公差の利点

幾何公差を設計図面に適用することには、多くの利点があります。

• 機能性の明確化: 部品の機能に直接関連する幾何学的要件を明確に定義できるため、設計意図が製造部門や検査部門に正確に伝わります。
• 公差の最適化: 部品の機能に必要な精度のみを規定できるため、不必要に厳しい公差を避けることができ、製造コストの削減につながります。
• 設計の自由度向上: 従来の寸法公差では制約が大きかった設計においても、幾何公差を用いることで、より柔軟な設計が可能になります。
• 製造と検査の効率化: 明確な公差基準があることで、製造部門は目標とする品質レベルを理解しやすくなり、検査部門は合否判定を客観的に行うことができます。
• 国際的なコミュニケーションの円滑化: ISOなどの国際規格に準拠した幾何公差を用いることで、グローバルなサプライチェーンにおける部品の互換性や品質保証が容易になります。
• 組み立て性の向上: 幾何公差、特にMMCや投影公差域を適切に用いることで、部品の組み立て不良を低減し、スムーズな組み立て作業を実現できます。

幾何公差の適用における注意点

幾何公差は強力なツールですが、適切に適用するためにはいくつかの注意点があります。

• 設計意図の正確な理解: 幾何公差を適用する際には、部品の機能や組み立て要件を十分に理解し、それに基づいて適切な種類と値の公差を選択する必要があります。
• データムの適切な設定: データムは、部品の機能や測定の基準となる重要な要素です。適切なデータムを設定しないと、意図した公差管理が行えません。
• 公差域の明確な定義: 公差域の形状や大きさ、向きなどを明確に規定する必要があります。曖昧な定義は、製造や検査における混乱を招きます。
• 図面の可読性: 幾何公差の記号や注記は、図面上で明確に表示され、他の寸法や注記と混同しないように配慮する必要があります。
• 製造および検査技術の考慮: 設定した幾何公差が、実際の製造技術や検査技術で実現可能かどうかを考慮する必要があります。
• 教育と訓練: 設計者、製造者、検査者など、幾何公差に関わるすべての関係者が、その意味と適用方法を正しく理解している必要があります。

まとめ

幾何公差は、現代の精密機械設計および製造において不可欠なツールです。部品の機能性を最大限に引き出し、品質を保証し、コスト効率を高めるために、その基本概念、種類、適用方法を正しく理解し、効果的に活用することが重要です。設計者は、幾何公差を駆使して、より高品質で信頼性の高い製品を開発し、製造部門は、その意図を正確に理解して、図面通りの部品を製造し、検査部門は、客観的な基準に基づいて品質を評価することが求められます。幾何公差の適切な適用は、製品開発から生産、品質管理に至るまでのすべての段階において、大きなメリットをもたらすでしょう。